During the EU CodeWeek 2023 Hackathon award ceremony the fair division algorithms were introduced as examples of practical application of algorithms in everyday life. EU CodeWeek strives to introduce algorithmic thinking and coding in schools.
Προ αμνημονεύτων ετών, με τον ξάδερφο μου το Διονύση ένα σημαντικό ζήτημα ήταν πώς να μοιραστούμε μια μερίδα τηγανητές πατάτες. Για να αποφύγουμε γκρίνιες και καβγάδες δοκιμάσαμε διάφορους τρόπους, π.χ. να παίρνουμε μία-μία, που αποδείχτηκε μη πρακτικό, ή να μας τις χωρίζει ένας μεγάλος, που δεν έδινε σημασία και δεν είχαμε εμπιστοσύνη στο αποτέλεσμα. Έτσι καταλήξαμε στον παλιό και δοκιμασμένο αλγόριθμο, ένας μοιράζει, άλλος επιλέγει.
Πράγματι, όποιος κάνει το μοίρασμα θα επιδιώξει να χωρίσει τις πατάτες στα μισά, γιατί αν υπάρχει ανισορροπία στις ποσότητες, ο άλλος που θα κάνει την επιλογή, θα επιλέξει το μεγαλύτερο. Για δύο άτομα, ο αλγόριθμος είναι λουκούμι: είναι ορθός, απλός, πρακτικός, κατανοητός και συνεπώς αποδεκτός.
Το πρόβλημα
Τώρα που είδαμε τη λύση, ας περιγράψουμε τι προσπαθούμε να πετύχουμε. Έχουμε να διαιρέσουμε ένα αγαθό, πχ. τις τηγανητές πατάτες ή ένα κέικ. Υπάρχουν οι συνδαιτημόνες που επιθυμούν να αποκτήσουν όσο το δυνατόν περισσότερο, αλλά θα συμβιβαστούν αν μπορέσουν να αποκτήσουν τουλάχιστον το κομμάτι που τους αναλογεί. Για ανθρώπους, αυτό σημαίνει ότι μετά τη μοιρασιά, καθένας τους πρέπει να έχει την αίσθηση ότι απέκτησε για τον εαυτό του ποσότητα τουλάχιστον
του αγαθού. Αυτή είναι η αρχή της Αναλογικότητας.
Σα να μην έφτανε αυτό, οι δικαιούχοι του αγαθού θα ήθελαν κανείς άλλος να μην πάρει κομμάτι μεγαλύτερο από το δικό τους. Δηλαδή, δεν μου αρκεί να πάρω (αυτό που κρίνω ως) δίκαιο μερτικό για πάρτη μου, αλλά δεν θέλω και κάποιος άλλος να πάρει κάτι περισσότερο από εμένα – ακόμη κι αν το στερεί από κάποιον τρίτο, γιατί θα τον ζηλεύω. Αυτή είναι η αρχή Δίχως-Φθόνο.
Ιδανικά, καθώς καταλαβαίνετε, μια δίκαιη μοιρασιά που σέβεται τις δυο αυτές αρχές θα αποδώσει ποσότητα ακριβώς σε όλους τους
δικαιούχους.
Σημείωση: Μια μοιρασιά μπορεί να είναι αναλογική και ωστόσο φθονερή (για ). Αντίθετα, μια μοιρασιά Δίχως-Φθόνο δεν μπορεί παρά να είναι Αναλογική.
Παρεμπιπτόντως, λύσεις του στιλ χρησιμοποίησε μια ζυγαριά ή ένα δικαστή για τη μοιρασιά δεν θεωρούνται έγκυρες λύσεις του προβλήματος, διότι βασίζονται σε μια έμπιστη εξωτερική οντότητα, στην οποία οι δικαιούχοι θα έπρεπε a priori να αναγνωρίσουν ως ανυστερόβουλη (ρε μπας και τα έχει κάνει πλακάκια με τους υπόλοιπους;) και να δεσμευτούν ανέκκλητα ότι θα αποδεχτούν τη μοιρασιά της.
Κινούμενο μαχαίρι
Για δίκαια μοιρασιά ανάμεσα σε δυο ανθρώπους, οκέι βρήκαμε τον ιδανικό αλγόριθμο, ο οποίος ωστόσο, δυστυχώς, δεν γενικεύεται για περισσότερους ανθρώπους (τσεκάρισέ το). Ας δούμε τι γίνεται όταν θέλουμε να μοιράσουμε ένα κέικ σε τρεις ανθρώπους.
Για τις περιπτώσεις όπου μια έξυπνη λύση είναι το ‘κινούμενο μαχαίρι‘: κάποιος τοποθετεί ένα μαχαίρι πάνω στο ένα άκρο του κέικ και αρχίζει να το κινεί αργά και σταθερά κατά μήκος του μεγαλώνοντας σταδιακά το τμήμα του κέικ που έχει προσπεράσει. Όποτε κάποιος από τους δικαιούχους θεωρήσει ότι το τμήμα είναι αρκετό, φωνάζει ‘κόψε’, και υποχρεωτικά το παίρνει. Η διαδικασία συνεχίζεται για τους υπόλοιπους. Έτσι όλοι είναι ικανοποιημένοι με το κομμάτι που πήραν – κατ’ επιλογή τους. Ακόμη κι ο τελευταίος, που δεν είπε ‘κόψε’ (θεωρώντας ότι κανένα από τα
κομμάτια των προηγούμενων δεν ήταν αρκετά μεγάλο), πρέπει να είναι ικανοποιημένος με το εναπομείναν τμήμα του κέικ που κατά την εκτίμησή του είναι μεγαλύτερο από
, δηλαδή
.
Το κινούμενο μαχαίρι (Dubins και Spanier, 1961) εξασφαλίζει αναλογική μοιρασιά. Ωστόσο, ένας ζηλιάρης που έχει ήδη πάρει το κομμάτι του, κατά την περαιτέρω εξέλιξη της κατάτμησης πρέπει να απόσχει: ακόμη κι αν θεωρήσει ότι ένα κομμάτι είναι μεγαλύτερο από αυτό που έχει ήδη πάρει, δεν μπορεί να το διεκδικήσει. Άρα ο αλγόριθμος δεν εξασφαλίζει την αρχή Δίχως-Φθόνο.
Μοιρασιά στα τρία Δίχως-Φθόνο
Μπορούμε να μοιράσουμε σε τρεις καλύτερα από το κινούμενο μαχαίρι; Οι Selfridge και Conway ανακάλυψαν έναν τρόπο ήδη το 1960, αλλά δεν έκριναν ότι αξίζει να τον δημοσιεύσουν! Πάει ως εξής:
- Ο Α τεμαχίζει το κέικ σε 3 ίσα, κατά την εκτίμησή του, κομμάτια.
- Ο Β εκτιμά ποιο είναι μεγαλύτερο και αποκόπτει το υπερβάλλον τμήμα του, τόσο όσο να μην είναι μικρότερο από τα άλλα δύο κομμάτια.
- Ο Γ επιλέγει ένα από τα τρία κομμάτια – όποιο γουστάρει.
- Αν ο Γ επέλεξε το κομμάτι που μίκρυνε στο βήμα (2), τότε ο Β επιλέγει ανάμεσα στα άλλα δύο κομμάτια. Διαφορετικά, ο Β παίρνει υποχρεωτικά το κομμάτι που μίκρυνε ο ίδιος στο βήμα (2).
- Ο Α παίρνει το (ακέραιο) κομμάτι που έχει απομείνει.
Μέχρι εδώ οι τρεις παίκτες είναι ικανοποιημένοι με τα κομμάτια που πήραν και δίχως φθόνο αναμεταξύ τους. Αλλά μένει το απόκομμα, για το οποίο:
- Ο παίκτης που δεν πήρε το κομμάτι από το οποίο είχε αφαιρεθεί το απόκομμα (είναι ο Β ή ο Γ), τεμαχίζει το απόκομμα σε 3 ίσα, κατά την εκτίμησή του, κομμάτια.
- Ο έτερος των Β ή Γ επιλέγει κομμάτι πρώτος.
- Ο παίκτης Α επιλέγει δεύτερος.
- Ο παίκτης του βήματος (6) επιλέγει τρίτος και καταϊδρωμένος.
Δεν είναι προφανές, αλλά και σε αυτό το στάδιο η μοιρασιά είναι αναλογική και δίχως φθόνο, ακόμη και για τον παίκτη Α στο βήμα (8). Παρότι πληροί τις προδιαγραφές που θέσαμε στην αρχή, ο αλγόριθμος δεν είναι προφανής – άσε που οι παίκτες θα φάνε τρίμματα αφού το κέικ μπορεί να κοπεί σε 6 κομμάτια. Δυστυχώς, ο αλγόριθμος δεν γενικεύεται για περισσότερους από 3 ανθρώπους.
Επίλογος
Μόλις το 1995 οι Brams και Taylor κατασκεύασαν τον πρώτο αλγόριθμο για οσουσδήποτε παίκτες που είναι και Δίχως-Φθόνο. Ωστόσο, είναι πολύπλοκος και απαιτεί πολλά βήματα, π.χ. για μοίρασμα σε 4 παίκτες απαιτεί 20 βήματα. Το χειρότερο είναι ότι δεν έχει άνω φράγμα για το πλήθος των βημάτων. Ακόμη χειρότερα, το καλύτερο όριο πολυπλοκότητας που έχει βρεθεί μέχρι τώρα για το πρόβλημα της δίκαιης μοιρασιάς ανάμεσα σε παίκτες είναι, κρατηθείτε..
Ευχαριστώ, δεν θα πάρω.
Για κλείσιμο –δεν κρατιέμαι– ποιος άραγε πρότεινε τον συμβολισμό με τα πάνω βελάκια για την επαναλαμβανόμενη ύψωση σε δυνάμεις; Knuth, 1976
Αναφορές
- Subhash Suri, Fair Division and Cake Cutting, February 27, 2020
- Ulle Endriss, Lecture Notes on Fair Division, Institute for Logic, Language and Computation, University of Amsterdam, 7 April 2010
- Fair cake-cutting – Wikipedia

























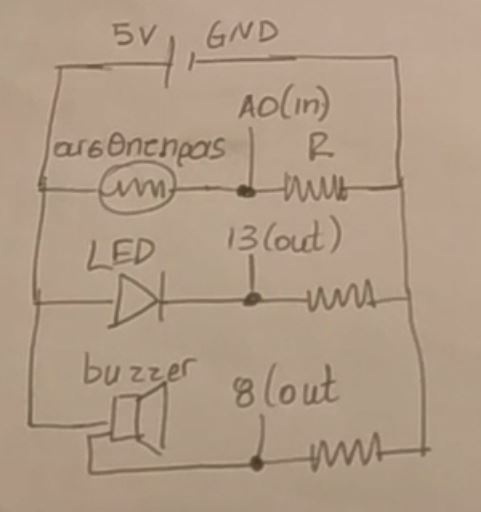
 Αν η τιμή της είναι πάνω από ένα κατώφλι, ανάβει το ενδεικτικό LED, αλλιώς το σβήνει.
Αν η τιμή της είναι πάνω από ένα κατώφλι, ανάβει το ενδεικτικό LED, αλλιώς το σβήνει.