Παραγοντικό και Γάμμα

Τετάρτη, 23/08/2023 by igaviotis

Στο σχολείο δε νομίζω οτι είχαμε μιλήσει καθόλου για το παραγοντικό. Άρα υποθέτω ότι το είδα πρώτη φορά στη σχολή, στο μάθημα Προγραμματισμός ΙΙ, όταν μαθαίναμε για τις αναδρομικές κλήσεις συναρτήσεων στην Pascal (εμ βέβαια, στο Προγραμματισμός Ι κάναμε FORTRAN, τρομάρα μας, τι αναδρομή και πράσινα άλογα).

Εδώ θα δούμε διαδοχικές επεκτάσεις του παραγοντικού από τους ακέραιους, στους πραγματικούς και στους μιγαδικούς. Ακροθιγώς θα αναφέρω ενδεικτικές εφαρμογές του. Αφορμή για το mash up άρθρο αυτό στάθηκε η κουκλίστικη ομορφιά της συνάρτησης Γάμμα.

Ακέραιοι

Με πόσους διαφορετικούς τρόπους μπορούν να τερματίσουν 4 ποδηλάτες Α, Β, Γ, Δ; Πρώτος μπορεί να είναι καθένας από τους τέσσερις, και θα ακολουθούν οι υπόλοιποι τρεις. Έτσι αναγουμε το αρχικό ερώτημα στο ίδιο μικρότερου μεγέθους. Για 1 ποδηλάτη, υπάρχει 1 τρόπος τερματισμού· για 2 ποδηλάτες είναι 2, ΑΒ ή ΒΑ· για 3 ποδηλάτες είναι 6 οι τρόποι τερματισμού, ΑΒΓ, ΑΓΒ, ΒΑΓ, ΒΓΑ, ΓΑΒ, ΓΒΑ. Άρα για τους 4 ποδηλάτες, έχουμε 4*6 = 12 αναδιατάξεις, όπως τις λέμε στα διακριτά μαθηματικά. Για $n$ ποδηλάτες είναι τόσες αναδιατάξεις ώστε οποιοσδήποτε από τους $n$ να είναι πρώτος, ακολουθούμενος από τους υπόλοιπους $n-1$ .

Ως σύμβολο του παραγοντικού, το θαυμαστικό $n!$ πρωτοχρησιμοποιήθηκε το 1808:

$4!=4 \cdot 3! = 4 \cdot 3 \cdot 2! = 4 \cdot 3 \cdot 2 \cdot 1! = 4 \cdot 3 \cdot 2 \cdot 1 =24$

Γενικά, για τους θετικούς ακέραιους, το παραγοντικό ορίζεται

$n! = \left\{ \begin{array}{ll} n \cdot (n-1)!, & n \geq 1\\ 1, &n=0 \end{array} \right. , n \in \mathbb{N}$

και στη μη αναδρομική εκδοχή του

$n! = n \cdot (n-1) \cdot (n-2) \cdots 1 = \prod_{i=1}^{n}i$

Πραγματικοί

Θα θέλαμε να επεκτείνουμε το παραγοντικό στους πραγματικούς αριθμούς! Δηλαδή θα θέλαμε μια συνάρτηση $f(x) = x \cdot f(x-1)!$ , για κάθε $x \in \mathbb{R}$ . Όταν το $x$ τυχαίνει να είναι ακέραιος, η τιμή αυτής της συνάρτησης ιδανικά θα ταυτίζεται με το ‘κανονικό’ παραγοντικό που ορίσαμε παραπάνω.

Είναι καταπληκτικό ότι υπάρχει μια τέτοια συνάρτηση! Λέγεται συνάρτηση Γάμμα

$\Gamma(x) = \int_0^\infty {t^{x - 1} e^{ - t} dt}$

Πατέρας της $\Gamma (x)$ είναι ο Euler γύρω στα 1730, αν και βρίσκουμε ανακατεμένα στην ιστορία τα μεγάλα ονόματα, όπως Bernoulli, Goldbach, Gauss.

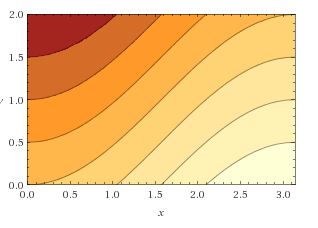
Υπάρχει μια ενοχλητική μετατόπιση κατά +1, αλλά ισχύει $\Gamma (n+1) = n!$ για τους θετικούς, όπως (δια)φαίνεται στο διάγραμμα Matlab

Πράγματι βλέπουμε Γ(1)=1=0!, Γ(2)=1=1!, Γ(3)=2=2!, Γ(4)=6=3!. Και αναλυτικά, για πχ $x=2$ με παραγώγιση κατά μέλη και εφαρμογή του κανόνα de l’Hôpital

$\Gamma( 2) = \int_0^\infty {t^{2 - 1} e^{ - t} dt} = \int_0^\infty {t e^{ - t} dt} = - e^{-t}(1+t)\big|_0^\infty = - \frac{t+1}{e^{t}}\big|_{0}^\infty = - \frac{1}{e^{t}}\big|_{0}^\infty = 1$

Αλλά το πιο σημαντικό είναι ότι

$\Gamma (x+1) = \int_0^\infty {t^{x} e^{ - t} dt} = -t^x e^{-t} \big|_0^\infty + x \int_0^\infty t^{x-1} e^{-t} dt = x \cdot \Gamma(x)$

υπό την προϋπόθεση ότι το $x$ είναι θετικό (για να μηδενιστεί ο πρώτος όρος του αθροίσματος).

Στις ενδιάμεσες πραγματικές μη-ακέραιες τιμές, η συνάρτηση συμπεριφέρεται φυσιολογικά (συνεχής). Το τοπικό ελάχιστο είναι στο σημείο [1.461632, 0.885603].

Μπορεί να φαίνεται ουρανοκατέβατο ότι από το ολοκλήρωμα της συνάρτησης Γάμμα προκύπτουν τιμές παραγοντικών – μια λογική και συνεπής εξήγηση στο Unraveling the Mystery Behind This Math Miracle – YouTube. Ως υπόδειξη, η νιοστή παράγωγος του μονωνύμου $x^n$ είναι

$\frac{d^n}{dx^n}(x^n) = n(n-1)(n-2) \cdots 2 \cdot 1 = n!$

Παραγοντικό αρνητικών ακεραίων

Αφού $0!=1$ και $n!=n(n-1)!$ , άρα $0! = 0 \cdot (-1)! = 1$ , δηλαδή το (-1)! πρέπει πολλαπλασιαζόμενο με το 0 να δίνει 1, που αναδίνει μια αίσθηση άπειρου. Με τους αρνητικούς ακέραιους θα πρέπει να περιμένουμε εκπλήξεις και από τη συνάρτηση Γάμμα, αφού αυτή ακολουθεί με συνέπεια τη συμπεριφορά του παραγοντικού.

Πράγματι, όσο λογικά και καλόβολα συμπεριφέρεται η συνάρτηση Γάμμα στους θετικούς πραγματικούς, τόσο στρυφνή και πηδηχτούλα γίνεται στους αρνητικούς:

Η συνάρτηση Γάμμα στους πραγματικούς (αρνητικούς και θετικούς)

Για παράδειγμα, στις ακέραιες αρνητικές τιμές -1, -2, .., όχι μόνο είναι ασυνεχής, αλλά πηδάει από το $-\infty$ στο $+\infty$ , ή πιο ορθά η συνάρτηση Γάμμα έχει singularities (or “simple poles”).

Πάντως η Γάμμα παραμένει πραγματική για στους πραγματικούς – θετικούς κι αρνητικούς, εκτός πόλων. Και το λέω αυτό γιατί τώρα θα προχωρήσουμε στην..

Επέκταση στους μιγαδικούς

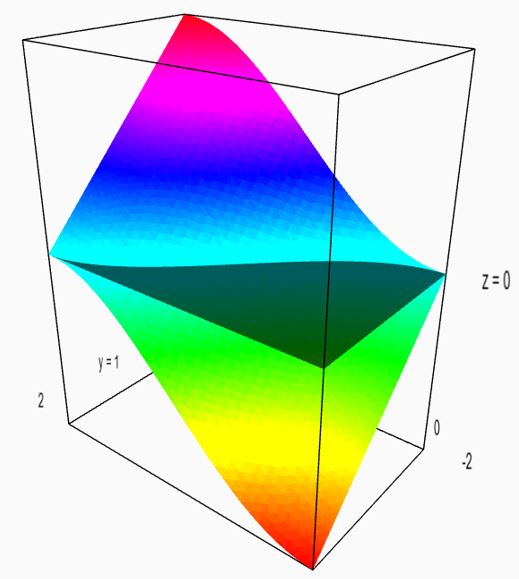
Ας γίνουμε πιο τολμηροί. Γιατί να μην επεκτείνουμε το πεδίο ορισμού της συνάρτησης Γάμμα στους μιγαδικούς;

$\Gamma(z) = \int_0^\infty {t^{z - 1} e^{ - t} dt}, z \in \mathbb{C}$

Στα σημεία όπου $\Re(z) \in \mathbb{Z}^{-}, \Im(z)=0$ έχει τους πόλους που είδαμε παραπάνω και απεικονίζονται ξεκάθαρα στην γραφική παράσταση του μέτρου $| \Gamma(z) |$ , δηλ. της απόστασης από την αρχή των αξόνων:

Στους δύο άξονες το πραγματικό και το φανταστικό μέρος του πεδίου ορισμού και στον ‘κατακόρυφο’ άξονα το μέτρο της $\Gamma(z)$

Τιμές και τύποι της συνάρτησης Γάμμα

Για τους θετικούς ακέραιους, η συνάρτηση Γάμμα ταυτίζεται με το παραγοντικό

$\Gamma(n+1) = n!, \; n \in \mathbb{N}$

Στους μιγαδικούς ο καθοριστικός τύπος είναι

$\Gamma(z+1) = z \cdot \Gamma(z)$

Ένας εντυπωσιακός ανακλαστικός τύπος για τη συνάρτηση Γάμμα είναι

$\Gamma(z) \cdot \Gamma(1-z) = \frac{\pi}{sin(\pi z)}, \; z \notin \mathbb{Z}$

από όπου προκύπτει

$\Gamma(\frac{1}{2}) \cdot \Gamma(1-\frac{1}{2}) = (\Gamma(\frac{1}{2}))^2 = \frac{\pi}{sin(\pi / 2)} = \pi \Rightarrow \Gamma(\frac{1}{2}) = \sqrt{\pi}$

Γουστάρω που ανακακατεύονται παραγοντικό, μιγαδικοί, ολοκληρώματα και ξεπηδάνε ρίζα, τριγωνομετρική συνάρτηση και το $\pi$ .

Γενικεύοντας, για τα μισά των θετικών ακεραίων παίρνουμε κατηφορικά την αναδρομή και σταματάμε στο $\Gamma(1/2)$

= (\frac{1}{2}+n-1) \cdot \Gamma(\frac{1}{2}+n-1)

Οι τιμές αυτές αυξάνουν μονότονα απειριζόμενες, αφού το γινόμενο των $n$ μονών όρων του αριθμητή άνετα νικά το $2^n$ του παρονομαστή, και σωστά, αφού οι τιμές πρέπει να κινούνται μέσα στο $[n!, (n+1)!]$

Τώρα, τα μισά των αρνητικών ακεραίων ξεκινούν με

$\Gamma(- \frac{1}{2}) = \frac{ \Gamma(\frac{1}{2})} {- \frac{1}{2}} = -2 \sqrt{\pi}$

και κατηφορίζουν ως

$\Gamma(-\frac{1}{2}-n) = \frac{\Gamma(-\frac{1}{2} -n+1)}{-\frac{1}{2}-n} = \cdots = \frac{\Gamma(-\frac{1}{2}-n+n)}{(-\frac{1}{2}-n) \cdot (-\frac{1}{2}-n+1) \cdots (-\frac{1}{2}-n+n-1)} = \frac{\Gamma(-\frac{1}{2})}{(-1)^n \cdot \frac{2n+1}{2} \cdot \frac{2n-1}{2} \cdots \frac{3}{2}}$

που αντικαθιστώντας κάνει

$\Gamma(-\frac{1}{2}-n) = \frac{(-2)^{n+1}}{ (2n+1) \cdots 5 \cdot 3 \cdot 1} \cdot \sqrt \pi = (-1)^{n+1} \cdot \frac{2^{2n+1} \cdot n!}{(2n+1)!} \cdot \sqrt \pi$

Οι τιμές της Γάμμα για τα αρνητικά μισά εναλλάσσουν πρόσημο και τείνουν στο 0 όσο κατεβαίνουμε προς το $-\infty$ .

Ανακεφαλαιώνοντας, για τα σημεία ±X.5

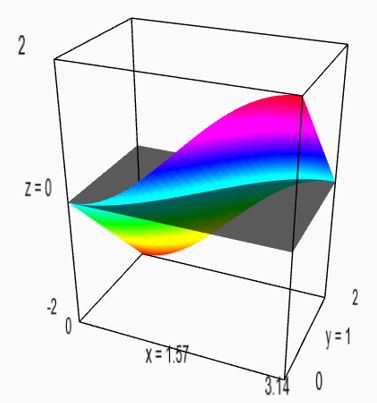
Ας ψαχουλέψουμε λίγο τις μιγαδικές τιμές που παίρνει η $\Gamma(z)$ όταν το $\Im(z) \ne 0$ . Για παράδειγμα, μπορούμε να υπολογίσουμε αριθμητικά

$i! = \Gamma(i+1) = 0.49802 - 0.15495i$

Αν εξαιρέσουμε την περιοχή γύρω από τους πόλους, στους μιγαδικούς αριθμούς με αρνητικό πραγματικό μέρος, η Γάμμα είναι αρκετά ομαλή και μάλιστα όσο μεγαλώνει κατ’ απόλυτη τιμή το πραγματικό μέρος, η αναστάτωση του πόλου συρρικνώνεται όλο και πιο κοντά του.

Για αρνητικά, όχι ακέραια $\Re (z)$ , όσο το $\Im (z)$ απομακρύνεται από το 0, η συνάρτηση παίρνει μικρές τιμές, τόσο κατά το πραγματικό, όσο και κατά το φανταστικό της μέρος, ενώ ξεσαλώνει κοντά στα ακέραια πραγματικά μέρη και η κατάσταση οξύνεται όσο μικραίνει το φανταστικό μέρος.

Εχ, μακάρι να βλέπαμε τετραδιάστατα για να την απολαύσουμε σε όλο το μεγαλείο της.

Εναλλακτική μορφή

Αυτοί που έχουν αλλεργία στα ολοκληρώματα, μπορεί να εκτιμήσουν έναν εναλλακτικό τύπο για το παραγοντικό. Ο Euler τον δημοσίευσε στις 13 Οκτωβρίου 1729, αλλά επειδή δεν του άρεσε το γινόμενο, προχώρησε και βρήκε στις 8 Ιανουαρίου 1730 τον τύπο με το ολοκλήρωμα που είδαμε παραπάνω.

Σκιαγράφοντας πώς προκύπτει, από το How to Take the Factorial of Any Number – YouTube, με λογαρίθμηση του γενικευμένου παραγοντικού τα γινόμενα μετατρέπονται σε αθροίσματα και επιτρέπεται μια γραμμική προσέγγιση επειδή ο λογάριθμος έχει κόψει τη φόρα του παραγοντικού

$(x+n)! = x! \cdot (x+1)(x+2) \cdots (x+n) \Rightarrow$

$\ln((x+n)!) = \ln(x!) + \sum_{i=1}^n \ln(x+i) \approx \ln(x!) + x \ln n$

Σουτάροντας τα όρια στο άπειρο, η προσέγγιση γίνεται ισότητα

$\ln(x!) = \lim\limits_{n \to \infty}\bigl\{ \sum_{i=1}^n \ln i - \sum_{i=1}^n \ln(x+i) + x\ln n \bigl\}$

$= \lim\limits_{n \to \infty}\bigl\{ \sum_{i=1}^n \ln\frac{i}{x+i} + x \ln n \bigl\}$

Τέλος, ύψωση σε δύναμη για να ξεφορτωθούμε το λογάριθμο

$x! = \lim\limits_{n \to \infty}\bigl\{ e^{x\ln n + \sum_{i=1}^n ln \frac{i}{x+i} } \bigl\} = \lim\limits_{n \to \infty}\bigl\{n^x \cdot \prod_{i=1}^n \frac{i}{x+i} \bigl\}$

Για λόγους ιστορικής ακρίβειας, πρώτος ο Bernoulli, μία εβδομάδα νωρίτερα από τον Euler, στις 6 Οκτωβρίου 1729, είχε δημοσιεύσει έναν παρόμοιο τύπο με γινόμενο

$\lim\limits_{n \to \infty}\{(n+\frac{x}{2})^{x-1} \cdot \prod_{i=1}^{n-1}\frac{i+1}{x+i}\}$

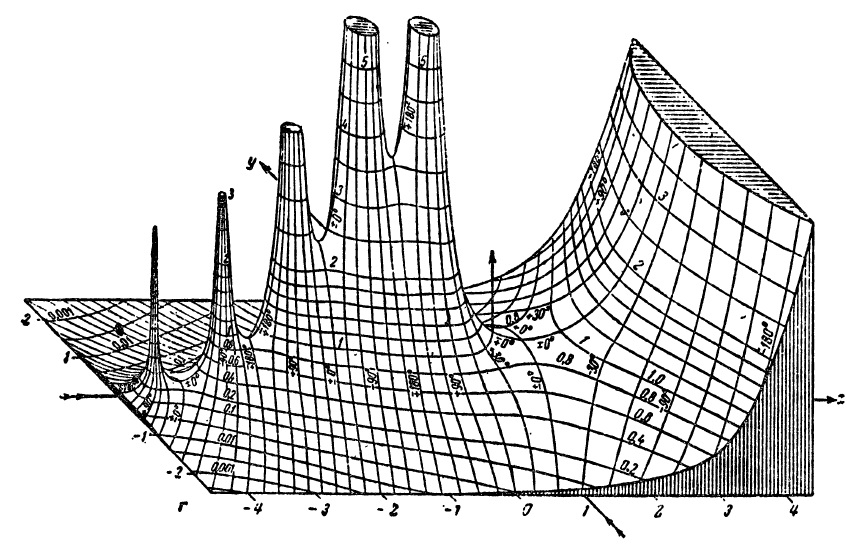
Για το τέλος, απολαύστε μια χειροποίητη απεικόνιση του μέτρου της συνάρτησης Γάμμα από το 1909:

A hand-drawn graph of the absolute value of the complex gamma function, from Tables of Higher Functions by Jahnke and Emde.

Αντίστροφο παραγοντικό

Και ενώ το είχα κλείσει το blogpost, βγάζει ο Michael Penn το Do you know about the «reciprocal gamma function»?? – YouTube, όπου εξετάζει μια ειδική μορφή του ολοκληρώματος που χρησιμοποιείται στο μετασχηματισμό Laplace.

Το ολοκλήρωμα

$L(s) = \frac{1}{2\pi} \int_{-\infty}^{\infty}\frac{e^{1+it}}{(i+it)^s}dt$

με ολοκλήρωση κατά μέλη πάνω στην $(1+it)^{-n}$ , δίνει την αναδρομή

$L(n+1) = \frac{1}{n} L(n)$

και αφού μετά κόπων και βασάνων αποδεικνύεται $L(2)=1$ , προκύπτει ότι

$L(3)=\frac{1}{2}, L(4)=\frac{1}{3 \cdot 2}, L(5)=\frac{1}{4!}, \cdots L(n+1)= \frac{1}{n!}, \; n \in \mathbb{N}$

Με απλά λόγια, το ολοκλήρωμα αυτό μας δίνει τα αντίστροφα των παραγοντικών:

Διάγραμμα των αντίστροφων παραγοντικών και άλλες σχετικές συναρτήσεις

Παπούτσια στη σειρά

Πέμπτη, 08/04/2021 by igaviotis

Γιατί άραγε χρειάζεται τόση προσπάθεια για να κρατηθεί το σπίτι σε τάξη; Αυτό το θεμελιώδες ζήτημα με απασχόλησε στο «Καπάκι της οδοντόπαστας» και το προσεγγίζω κι εδώ με ένα άλλο παράδειγμα.

Στην είσοδο του σπιτιού βγάζω τα παπούτσια και φοράω παντόφλες. Τα παπούτσια κανονικά πρέπει να είναι τοποθετημένα στη σειρά κατά ζευγάρι για να μπορώ να τα βάλω φεύγοντας. Ε, ποτέ δεν είναι. Γιατί;

Ερώτημα

Έχετε τρία διαφορετικά ζευγάρια παπούτσια. Ποια είναι η πιθανότητα να είναι σωστά τοποθετημένα στη σειρά (δηλαδή αριστερό-δεξί πλάι-πλάι);

Απάντηση

Όλα τα ζευγάρια είναι διαφορετικά και τα δυο παπούτσια του ίδιου ζευγαριού είναι αριστερό και δεξί, άρα διαφορετικά μεταξύ τους. Άρα έχουμε 6 διαφορετικά παπούτσια και υπάρχουν $6!=6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1=720$ δυνατοί τρόποι τοποθέτησής τους (αναδιατάξεις). Σε αυτούς τους τυχαίους τρόπους διάταξης, στους περισσότερους τα παπούτσια είναι ανακατωμένα.

Ας μετρήσουμε σε ποιες διατάξεις είναι τακτοποιημένα σωστά τα παπούτσια: πρέπει να είναι αριστερά το αριστερό παπούτσι και δεξιά το δεξί του ίδιου ζευγαριού. Επειδή έχουμε 3 ζευγάρια παπούτσια και δεν έχει σημασία η σειρά των ζευγαριών μεταξύ τους, υπάρχουν $3!=3 \cdot 2 \cdot 1$ διατάξεις ζευγαριών.

Άρα η πιθανότητα να είναι τακτοποιημένα τα παπούτσια είναι $3!/6!= 6/720=1/120=0,0083$ , δηλαδή λίγο κάτω από 1%. Γι αυτό αν δεν τακτοποιήσω εγώ τα παπούτσια στη σειρά, μόνο 3 φορές το χρόνο θα είναι τακτοποιημένα από μόνα τους κατά τύχη.

Γενίκευση

Στη γενική περίπτωση που έχω $n$ ζευγάρια παπούτσια, η πιθανότητα να είναι στη σειρά είναι $n!/(2n)!$ Ο πίνακας δείχνει ότι οι πιθανότητες για αυτούς που έχουν μεγάλη παπουτσοθήκη είναι απογοητευτικές..

Πίνακας για $1,2, \cdots , n$ ζευγάρια παπουτσιών

Πρόγραμμα

Επειδή δεν είμαι μαθηματικός, ούτε και έχω πολλή αυτοπεποίθηση για τις ικανότητες μου στις Πιθανότητες, θα επαληθεύσω το αποτέλεσμα. Ακολουθεί κώδικας σε Python. Είναι ασυζητητί η πιο βολική γλώσσα, χάρη στην υποστήριξη που παρέχει για λίστες (ίσως και η Lisp).

import itertools, random
def sostaTopothetimena(stiSeira):
  for i in range(0, len(stiSeira), 2):
    enaPap, dyoPap = stiSeira[i], stiSeira[i+1]
    if not ((enaPap[0] == dyoPap[0]) and (enaPap[1] == 'Αριστερό') and (dyoPap[1] == 'Δεξί')):
      return False
    #print(stiSeira)
  return True

zevgariaPapoutsia = {'Αθλητικά', 'Μπότες', 'Μοκασίνι', 'Πέδιλα'}
zevgari = {'Αριστερό', 'Δεξί'}
papoutsia = list(itertools.product(zevgariaPapoutsia, zevgari))
sosta = 0
epanal = 1000000
for j in range(1, epanal):
  random.shuffle(papoutsia)
  if sostaTopothetimena(papoutsia):
    sosta += 1
print("Σχετική συχνότητα σωστών", sosta / epanal)

Ορίζω σε ένα σύνολο zevgariPapoutsia που έχω. Χρησιμοποιώ Python set για να επιβάλλω ότι όλα τα ζευγάρια είναι διαφορετικά, όπως στα κανονικά μαθηματικά σύνολα. Έτσι αν βάλεις δυο ίδια ζευγάρια ‘Αθλητικά’ θα τα αποθηκεύσει (ορθώς) μια φορά, διότι τα σύνολα δεν επιτρέπουν διπλότυπα στοιχεία. Θα μπορούσα να χρησιμοποιήσω εναλλακτικά Python list, αλλά δεν μου αρέσει γιατί στην επόμενη γραμμή παίρνω το καρτεσιανό γινόμενο των δυο συνόλων zevgariaPapoutsia και zevgari και κανονικά το καρτεσιανό γινόμενο εφαρμόζεται επί συνόλων, άσχετα πως στην Python θα μπορούσαν να είναι και λίστες. Το αποτέλεσμα της μεθόδου itertools.product το αποθηκεύω στη λίστα papoutsia και όχι σε σύνολο, διότι θέλω να την αναδιατάσσω και τα μαθηματικά σύνολα δεν ενέχουν διάταξη. Ορθώς η Python μπορεί να κάνει random.shuffle() σε list αλλά όχι σε set.

Μετά επαναλαμβάνω το πείραμα ένα εκατομμύριο φορές ώστε τα (στατιστικά) αποτελέσματά του να τείνουν προς το αναμενόμενο αποτέλεσμα (Νόμος των μεγάλων αριθμών).

Η βοηθητική μέθοδος sostaTopothetimena απλώς διατρέχει τα παπούτσια στη σειρά ανά δύο και ελέγχει αν ανήκουν στο ίδιο ζευγάρι και το ένα από αυτά είναι το αριστερό ενώ το άλλο είναι το δεξί.

Μια εκτέλεση του παραπάνω κώδικα για τέσσερα ζευγάρια παπούτσια δίνει:

Σχετική συχνότητα σωστών 0.000601

ή 0.0601% που είναι αρκετά κοντά στο αποτέλεσμα του παραπάνω πίνακα.

Διερεύνηση

Η πιθανότητα να είναι σωστά τοποθετημένα $n$ ζευγάρια παπουτσιών στη σειρά είναι

\frac{n!}{(2n)!} — Λίγες πράξεις δεν βλάπτουν..

= \frac{n!}{1 \cdot 2 \cdot 3 \dotsb (n-1) \cdot n \cdot (n+1) \dotsb (2n-1) \cdot(2n)} — Λίγες πράξεις δεν βλάπτουν..

Παραλλαγή

Αν μπαίνοντας στο σπίτι πετάω πιο προσεκτικά τα παπούτσια μου στην παπουτσοθήκη έτσι ώστε τα δυο παπούτσια του κάθε ζευγαριού να παραμένουν δίπλα-δίπλα, τότε αρκεί το αριστερό να είναι αριστερά και το δεξί να είναι δεξιά και τότε όλα τα ζευγάρια της παπουτσοθήκης θα είναι τακτοποιημένα. Ξεκάθαρα, η πιθανότητα να είναι τακτοποιημένο ένα ζευγάρι είναι $P(Z)=1/2$ (δηλαδή αριστερό-δεξί και όχι δεξί-αριστερό).

Άρα υπό την προϋπόθεση ότι τα παπούτσια κάθε ζευγαριού παραμένουν δίπλα-δίπλα, για να είναι τακτοποιημένη η παπουτσοθήκη μου, αρκεί καθένα από τα $n$ ζευγάρια να έχει το αριστερό του παπούτσι αριστερά και το δεξί δεξιά. Μιας και η διάταξη του κάθε ζευγαριού είναι ανεξάρτητη από τη διάταξη όλων των υπόλοιπων,

$P(Z_1 \cap Z_2 \cap \cdots \cap Z_n) =P(Z_1) \cdot P(Z_2) \dots P(Z_n) = \frac{1}{2^n}$

Έτσι για 3 ζευγάρια παπούτσια, αν τα παρατάω κάπως προσεκτικά, η παπουτσοθήκη θα είναι τακτοποιημένη με πιθανότητα $\frac{1}{2^3}=\frac{1}{8}=12,5\%$ , ενώ στην ορίτζιναλ εκδοχή η πιθανότητα ήταν $\frac{1}{120} =0,8\overline{3}\%$ . Με λίγη προσοχή βέλτιωσα τις πιθανότητες κατά $1 \cdot 3 \cdot 5 = 15$ φορές, ή στη γενική περίπτωση κατά $1 \cdot 3 \cdot 5 \dotsb (2n-1)$ φορές.

Το καπάκι της οδοντόπαστας

Παρασκευή, 17/02/2017 by igaviotis

Κάθε πρωί ανοίγω το σωληνάριο της οδοντόπαστας για να πλύνω τα δόντια μου και ακουμπάω το καπάκι στην εταζέρα του καθρέπτη που έχει μια ελαφρά κλίση προς τα εμπρός. Μερικές φορές το καπάκι κυλάει και πέφτει από το ράφι στο νιπτήρα. Όσο βουρτσίζω τα δόντια μου, αναρωτιέμαι πόσο πιθανό είναι να συμβεί αυτό;

etazera-f — Το σκηνικό στην εταζέρα του μπάνιου

Τα δεδομένα

Το καπάκι της οδοντόπαστας είναι το απομεινάρι από ένα χωνί με κομμένη μύτη. Οι μετρήσεις που μπορούμε να κάνουμε εύκολα στο καπάκι, πχ με ένα χάρακα ή με ένα παχύμετρο για μεγαλύτερη ακρίβεια, είναι:

η μεγάλη διάμετρος $D$ στην κυκλική μεγάλη βάση του (από κει που βιδώνει στο σωληνάριο),
η μικρή διάμετρος $d$ του κύκλου στο πάνω μέρος του καπακιού, και
το ύψος $h$ , δηλαδή η απόσταση ανάμεσα στη βάση και στο πάνω μέρος

pahimetro-f — Το καπάκι και το παχύμετρο

Οι αντίστοιχες ακτίνες είναι $R=D/2$ και $r=d/2$ . Το καπάκι όταν κυλάει (δεν ολισθαίνει) γράφει με τη βάση του κύκλο ακτίνας $G$ και με το πάνω μέρος μικρότερο κύκλο ακτίνας $g$ . Ας τα υπολογίσουμε.

Ο κύκλος

Τα τρίγωνα που σχηματίζονται προεκτείνοντας τη γενέτειρα είναι όμοια, άρα $\frac{g}{G} = \frac{r}{R} = \frac{d}{D}$ .

Από το τραπέζιο που απεικονίζει το καπάκι, εστιάζω στο πάνω τριγωνάκι για το οποίο ο Πυθαγόρας λέει:

$(G-g)^2 = (R-r)^2 + h^2$

όπου αντικαθιστώντας το $g$ με $\frac{r}{R}\cdot g$ , προκύπτει

$G = \frac{\sqrt{(R-r)^2 + h^2}}{1-\frac{r}{R}}$

Για να πέσει το καπάκι πρέπει τουλάχιστον το μισό να βγει έξω από την εταζέρα. Άρα μας ενδιαφέρει αν ο κύκλος ακτίνας $g'=(G+g)/2$ βγαίνει εκτός. Από δω και πέρα, χωρίς να χάνουμε τίποτα από τη γενικότητα, θεωρούμε το καπάκι ως μια σημειακή μπίλια δεμένη με ένα άκαμπτο σύρμα από το κέντρο του κύκλου σε ένα κεκλιμένο επίπεδο.

Η διαδρομή

Η κυκλική πορεία που θα διαγράψει το (σημειο)καπάκι καθορίζεται από τη γωνία $a$ όταν τοποθετείται αρχικά πάνω στην επιφάνεια της εταζέρας. Κατά σύμβαση, αν το καπάκι τοποθετηθεί έτσι ώστε η μεγάλη βάση του να βλέπει το άκρο της εταζέρας, είναι $a=0^{\circ}$ και δεν θα κουνηθεί καθόλου. Αντίθετα, όταν το πάνω μέρος του καπακιού αντικρύζει το άκρο της εταζέρας, η γωνία $a$ είναι $180^{\circ}$ και τότε διαγράφεται η μεγαλύτερη διαδρομή (ένα ημικύκλιο).

Ας διακρίνουμε τώρα δυο περιπτώσεις. Όταν το καπάκι τοποθετείται κάτω από την οριζόντια διακεκομμένη γραμμή, τότε η κατηφόρα μέχρι το κατώτερο σημείο της διαδρομής είναι $g' - g' \cdot \cos a$ . Όταν το καπάκι τοποθετείται στο πάνω ημικύκλιο κατηφορίζει υψομετρικά κατά $g' \cdot \cos (\pi-a) + g'$ ή απλούστερα $g' - g' \cdot \cos a$ . Α, τι ωραία, άρα η κατακόρυφη απόσταση που διανύει το καπάκι είναι

$f(a) = g' \cdot (1 - \cos a)$

για όλες τις γωνίες.

Έστω ότι το καπάκι τοποθετείται σε απόσταση $s$ από το άκρο της εταζέρας. Αν το $f(a)$ είναι μεγαλύτερο του $s$ , το καπάκι θα πέσει.

Η πραγματικότητα

Το πραγματικό καπάκι έχει διαμέτρους $D=17mm, d=14mm$ και ύψος $h=17mm$ .
Με τα παραπάνω προκύπτει κύκλος ακτίνας $G=96.7mm$ . Πειραματικά, ο κύκλος που γράφει το καπάκι έχει εξωτερική διάμετρο $2G \approx 200mm$ , που δίνει απόκλιση $< 4\%$ που την αποδίδω στην ακρίβεια των μετρήσεων με το παχύμετρο.

Προκύπτει $g'=88.17mm$ . Η εταζέρα έχει πλάτος $S=136mm$ . Ενδεικτικά, αν ακουμπήσω το καπάκι με γωνιά $a=\pi/2$ στο μέσο της εταζέρας $s=68mm$ , θα πέσει. Γι’ αυτό το κυνηγάω τόσο συχνά.

Πόσο συχνά;

Κάθε φορά που ακουμπάω το καπάκι, πρέπει να μετράω τη γωνία $a$ και την απόσταση $s$ από το άκρο και χρησιμοποιώντας το $g'$ που υπολόγισα, θα ξέρω με σιγουριά ότι αν το $f(a)-s$ είναι θετικό, το καπάκι πέφτει. Αλλιώς, κάνει πέρα-δώθε στην εταζέρα και μένει πάνω της. Μας φώτισες!

Στη σελίδα που υπολογίζει την καπακο-συμπεριφορα, έχω υλοποιήσει ένα πείραμα όπου για το συγκεκριμένο καπάκι (δεδομένη τροχιά) παίρνει όσα δείγματα του πεις για όλες τις γωνίες $a \in [0, \pi]$ και αποστάσεις $s \in [0, S]$ και υπολογίζει την πιθανότητα $f(a) > s$ , οπότε πέφτει το καπάκι. Επαναλαμβάνοντας το πείραμα πολλές φορές, προκύπτει ότι το καπάκι θα πέφτει με πιθανότητα $\approx 58,66\%$ . Βρέθηκε μια απάντηση στο αρχικό ερώτημα που τέθηκε, για οποιοδήποτε καπάκι και για οποιαδήποτε εταζέρα, αλλά είναι λίγο μπακάλικη (κομπιουτερική, για να το θέσω πιο κομψά…).

Γραφήματα

Ας το παιδέψω λίγο ακόμη. Όταν η συνάρτηση

$p(a,s)=g' \cdot (1 - \cos a) - s, a \in [0, \pi], s \in [0, S]$

είναι θετική, το καπάκι πέφτει. Για απλοποίηση, θέτω $S=2g'$ και $g'=1$ και προκύπτουν γραφήματα που δείχνουν ότι οι πιθανότητες να πέσει το καπάκι $50\%$ . Όσο το $S$ μικραίνει, τόσο ανεβαίνει προς τα πάνω ο γκρι κόφτης που φαίνεται στα γραφήματα

Τα γραφήματα τα έφτιαξα με το Sage με τον κώδικα

def p(a, s):
  return 1-math.cos(a)-s

def g(a,s):
  return 0

P = plot3d(p,(0, math.pi),(0, 2), adaptive=True, color=rainbow(160, 'rgbtuple'))
Q = plot3d(g,(0, math.pi),(0, 2), adaptive=True, color=(0,0,0), opacity=0.4)

show(P+Q)

Το μεταίχμιο μεταξύ πτώσης και πέρα-δώθε είναι εκεί που μηδενίζεται η συνάρτηση

$p(a, s) = 0 \Leftrightarrow s + \cos a = 1$

plot2d — Στις σκούρες περιοχές το καπάκι κάνει πέρα-δώθε, ενώ στις ανοικτόχρωμες πέφτει. Η καμπύλη που ξεκινά στο (0,0) και φτάνει στο (π,2) είναι το όριο.

Ας ολοκληρώσω για να ξεφορτωθώ τη γωνία

$\int_{0}^{\pi} p(a,s) da = \pi \cdot (g'-s)$

Άρα για μια τυχαία γωνία, οι πιθανότητες να πέσει το καπάκι εξαρτώνται αποκλειστικά από τη γεωμετρία του (το $g'$ ) και την απόστασή του από το άκρο της εταζέρας. Δεν ξέρω αν ήταν προφανές, αλλά αυτό δείχνει ότι η γωνιά είναι μια ανεξάρτητη μεταβλητή στο πείραμα. Ανεξαρτήτως γωνίας, το καπάκι θα πέφτει αν $g'>s$ , όπου τώρα τυχαία μεταβλητή έχει παραμείνει μόνο το $s$ που παίρνει τιμές στο $[0,S]$ .

Ας ξαναολοκληρώσω για να φύγει και το τυχαίο $s$ .

$\int_{0}^{S} \pi \cdot (g'-s) ds = \pi S (g' - S/2)$

$n \in \mathbb{N}$	$-\infty$	$-\frac{1}{2}-n$	$-1/2$	$1/2$	$\frac{1}{2}+n$	$\infty$
$\Gamma(n)$	$0$	$(-1)^{n+1} \cdot \frac{2^{2n+1} \cdot n!}{(2n+1)!} \cdot \sqrt \pi$	$-2 \sqrt \pi$	$\sqrt \pi$	$\frac{(2n)!}{4^n \cdot n!} \cdot \sqrt \pi$	$\infty$

Ζευγάρια παπουτσιών	$1$	$2$	$3$	$4$	$5$	$n$
Σωστές αναδιατάξεις	$1$	$2$	$6$	$24$	$120$	$n!$
Δυνατές αναδιατάξεις	$2$	$24$	$720$	$40.320$	$3.628.800$	$(2n)!$
Πιθανότητα	$50\%$	$8,\overline{3}\%$	$0,8\overline{3}\%$	$0,0595\dots\%$	$0,0033\dots\%$	$n!/(2n)!$

$\frac{n!}{(2n)!}$	$= \frac{n!}{1 \cdot 2 \cdot 3 \dotsb (n-1) \cdot n \cdot (n+1) \dotsb (2n-1) \cdot(2n)}$
	$=\frac{n!}{ \underbrace{1 \cdot 3 \cdot 5 \dotsb (2n-1)}_\text{odd} \cdot \underbrace{2 \cdot 4 \cdot 6 \dotsb (2n)}_\text{even} }$
	$= \frac{n!}{[1 \cdot 3 \cdot 5 \dotsb (2n-1)] \cdot 2^n \cdot [1 \cdot 2 \cdot 3 \dotsb n]}$
	$= \frac{n!}{[1 \cdot 3 \cdot 5 \dotsb (2n-1)] \cdot 2^n \cdot n!}$
	$= \frac{1}{[1 \cdot 3 \cdot 5 \dotsb (2n-1)] \cdot 2^n} = \frac{1}{2^n \cdot \prod_{k=0}^{n-1}(2k+1)}$

igaviotis

Stuff for sharing – Υλικό για μοίρασμα

Tag Archives: Μαθηματικά